Infix Expression Parsing
Compilers are complex beasts. In experimenting with writing my own recently, I’ve been exposed to a few of the elementary challenges in various stages of compilation. Having never written a compiler before, one of the first obstacles I ran into was expression parsing.
First, though, some introduction. Compilers, like most other types of software, are typically structured as a number of dependant modules. While the specific modularisation decisions vary from compiler to compiler, in theory there are around six basic stages in a traditional ‘source to object code’ translation. To briefly summarise these:
- Tokenization / Lexical Analysis: The stream of source code characters is broken up into meaningful phrases called ‘tokens’.
- Syntax Analysis: Tokens are checked against the grammar of the language, typically generating a ‘syntax tree’ from the token stream which defines the operations to be performed and their order.
- Semantic Analysis: The structure generated from syntax analysis is analysed further to ensure it makes sense. Type checking is often performed at this stage.
- Intermediate Code Generation: The tree structure representing the source program is translated into some other (typically low-level and machine-independent) representation.
- Code Optimisation: The intermediate representation is put through a number of passes to optimise it, typically to make the code more efficient (remove redundant operations, etc.).
- Code Generation: The intermediate representation is translated to the target assembly language.
Each of these stages contains some number of interesting problems to be solved, but I suspect the majority of people would agree that code optimisation and generation contain the most substantial challenges. In this post, however, I’m going to concentrate on the rather mature field of parsing. Particularly, parsing tokens into a syntax tree — that is, the syntax analysis stage.
A syntax tree, like any other tree, simply consists of a number of linked nodes. A syntax tree node representing the + operator might have children nodes which define the expressions to be added together, for example. Having this unambiguous representation of operations, and their order, turns out to be incredibly useful.
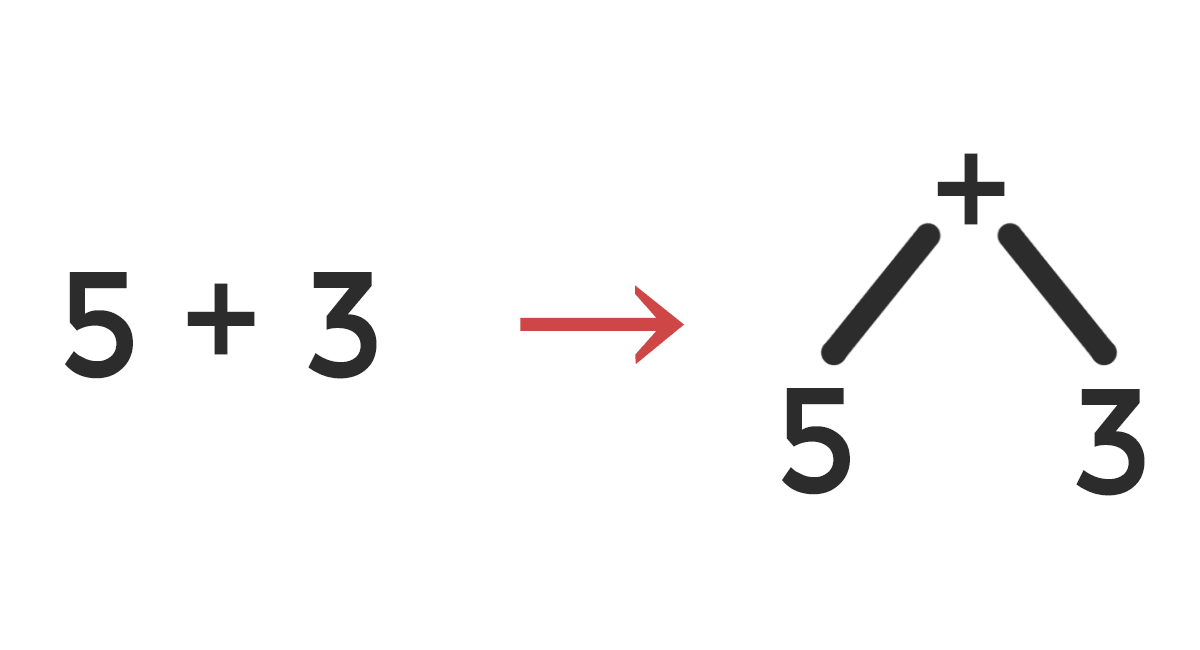
Top-down parsing is a method of parsing which attempts to build a syntax tree starting from a single root element by successively adding children nodes. A common method of top-down parsing is recursive descent, in which a number of procedures define each component (or ‘production’) of the grammar of the language. Furthermore, predictive recursive descent parsers perform recursive descent parsing by deciding what production to parse into the syntax tree next purely by looking ahead at what tokens follow. e.g. “I see the ‘var’ keyword, so it looks like I’ll be parsing a variable declaration into the syntax tree next!”.
A Naïve Expression Parser
So we’re writing a predictive recursive descent parser. Fundamentally our input is a bunch of tokens with ‘types’ and ‘values’, and our output is a syntax tree — often called an abstract syntax tree, or AST for short. Some structures are incredibly easy to parse with a parser of this kind. For example, we might parse (integer-only) variable declarations with something like the following:
ASTNode *parse_variable_declaration() {
consume_token(TOKEN_TYPE_KEYWORD, "int");
ASTNode *result = create_node();
result->type = NODE_TYPE_VARIABLE_DECLARATION;
result->children.left = parse_identifier();
result->children.right = NULL;
return result;
}
In the above I’m assuming that parse_identifier is another parser function that we’ve defined elsewhere, and — by definition — a NODE_TYPE_VARIABLE_DECLARATION typed AST node takes an identifier as its left child which should be declared as an integer variable. In in a real compiler we might also want to deal with the symbol table here, but we won’t worry about that in this post.
What if we wanted to parse expressions, though? Something like 5 + 5 + 1 shouldn’t be too hard, right? A naïve approach might be to simply recurse through all the binary operators in an expression and generate an appropriate syntax tree. For example:
ASTNode *parse_expression() {
ASTNode *result = parse_number();
if (peek_token_type(TOKEN_TYPE_OPERATOR)) {
ASTNode *operation = parse_operator();
operation->children.left = result;
operation->children.right = parse_expression();
result = operation;
}
return result;
}
Unfortunately, however, the above has a lot of problems. It just about works for the intended purpose — it’ll generate a correct syntax tree for simple additive expressions like 5 + 5 + 1 — but it can’t do much else particularly effectively. The main issues here are as follows.
Firstly, brackets. If we want to use brackets as part of an expression with the above implementation, it simply won’t parse correctly. This is relatively simple to fix by replacing parse_number with a call to parse_term, which can parse both numbers and bracketed expressions. If we want to support use of identifiers or unary operators in expressions, we can deal with those through parse_term too.
Secondly, precedence. While this method parses expressions with a single type of binary operator just fine, it doesn’t make any attempt to handle multiple levels of operator precedence. A multiplication operation won’t necessarily take place before an addition, for example. This might be an intentional design decision, in which case this isn’t a problem, but for most modern languages it’s probably just a failure in parser design.
Lastly, associativity. Though this approach just about holds up for addition operations, some operations require a certain operator associativity. Subtraction, for example, requires left associativity, as a - b - c is equal to (a - b) - c and not a - (b - c). Unfortunately, our approach generates the latter as the numbers parsed first will end up near the top of the syntax tree, not near the bottom, and so will be processed last.
In summary, this approach leaves a lot to be desired. In a more formal grammar notation, this naïve approach can be summarised with the following:
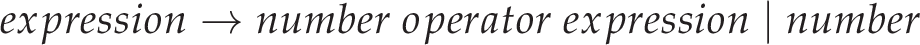
This reads in English as “an ‘expression’ is defined by a ‘number’ followed by an ‘operator’ followed by another ‘expression’, or alternatively is defined by a single ‘number’”. We narrowly avoided left-recursion — a source of infinite recursion in recursive descent parsing — by using expression → number operator expression instead of expression → expression operator number, but this is what resulted in the right associativity instead of left. We can do better than this.
Production Mangling
The two central problems that remain are essentially with associativity and precedence. If we consider the raw grammar for a moment without worry of left-recursion, and apply the previously discussed fix for bracketed expressions, we’re left with something like the following:
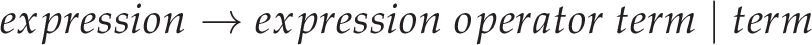

Introducing some precedence to this isn’t actually too difficult. We can simply add another layer of indirection such that additive expressions operate on multiplicative expressions which operate on ‘terms’. In a more proper terminology, we can add a multiplicative production to our language’s grammar:
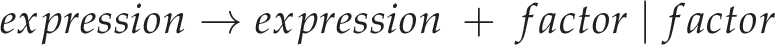
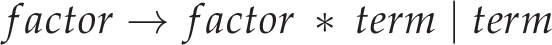
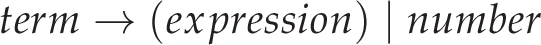
So ‘expressions’ are defined to be the addition of ‘factors’ (or just factors themselves), and ‘factors’ are defined to be the multiplication of ‘terms’ (or just terms themselves) — this way, multiplication has a higher precedence than addition! From here we would probably go ahead and add some more operators (namely, subtraction and division). On attempting to implement any of this using recursive descent, however, we’ll run into problems with left-recursion as alluded to previously.
There are some general techniques to remove left-recursion through the introduction of new language productions, but in this case we can simply do some reordering (much like the naïve solution). This change will also make things right associative, but we’ll worry about that later:
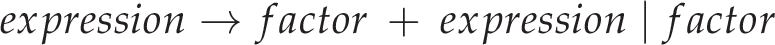
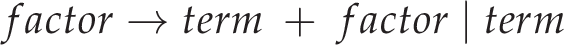
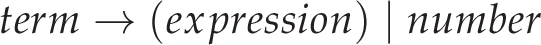
This solves the operator precedence problem… kind of. It’s not exactly easy to add new levels of precedence without doing an awful lot of faffing about, and all the recursive descent calls to different levels of precedence may become a performance issue with many operators. With a fixed set of operators, however, this likely isn’t a huge problem and so this solution may be perfectly suitable.
None of this really addresses the associativity problem either. In practise, it’s not too difficult to fix — we could simply use iteration to build AST nodes for left-associative operations in a bottom-up fashion, while continuing to build right-associative AST nodes in a top-down fashion. As bottom-up parsing naturally places tokens nearer the start of the token stream lower in the tree (as it builds the AST upwards), it is inherently suited for left-associativity. Again, for a fixed-operator environment this may be sufficient. In many cases, however, it would be nice to have a cleaner, more efficient, and more flexible process.
Precedence Climbing
One such solution to the problems outlined above is a method of expression parsing called precedence climbing. This has been used in the real world by projects such as Clang, and provides a cleaner method of dealing with both precedence and associativity correctly.
At its core, a precedence climbing expression parser parses infix expressions containing operators above some ‘minimum precedence’ level. At each stage, operators are added to the syntax tree either top-down via recursive methods or bottom-up via iterative methods, depending entirely on the associativity and precedence of the current operator being parsed. The code to implement this is something like the following:
ASTNode *parse_expression(int minimum_precedence) {
ASTNode result = parse_term();
while (peek_token_type(TOKEN_TYPE_OPERATOR) &&
peek_token_precedence() >= minimum_precedence) {
ASTNode *operation = parse_operator();
ASTNode *right = NULL;
int next_minimum_precedence;
if (operation->associativity == RIGHT_ASSOC) {
next_minimum_precedence = operation->precedence;
} else if (operation->associativity == LEFT_ASSOC) {
next_minimum_precedence = operation->precedence + 1;
} else {
error("Failed to parse operator without associativity.");
return NULL;
}
right = parse_expression(next_minimum_precedence);
// Add the 'right' child to build the tree top-down, and
// hoist up to 'result' to build the tree bottom-up.
operation->children.left = result;
operation->children.right = right;
result = operation;
}
return result;
}
The elegance in precedence climbing really comes from the coupled gains of both top-down and bottom-up parsing methods with regards to associativity and precedence. If you don’t quite understand how it works, I recommend tracing through the code with a few combinations of operators and examining the call stack.
If you’re interested in learning more about operator precedence parsing, it might be worth checking out the shunting-yard algorithm — a slightly more complicated alternative to precedence climbing — or looking at some of the solutions on the related wikipedia page.