OpenGL Matrix Transformation Order

Published October 23, 2013 By Joe Savage

When using OpenGL's matrix transformation functions (for example rotation, scaling, and translation), many newbies become confused as to why the transformations apply 'backwards'. The answer to this question is actually extremely simple if you know where to look, and lies in the matrices behind the code.

Matrices

First, a crash course in matrices (you can skip ahead if you already know this stuff). A matrix is just an array of numbers expressed in rows and columns. Take the following 2x3 matrix for example:

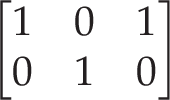
\begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}

The product of two matrices is the rows of the first matrix multiplied by the columns of the second (as such, the order of matrix multiplication does matter). An example of matrix multiplication is as follows:

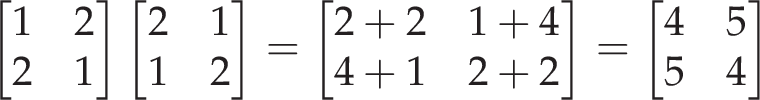
\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 2+2 & 1+4 \\ 4+1 & 2+2 \end{bmatrix} = \begin{bmatrix} 4 & 5 \\ 5 & 4 \end{bmatrix}

As a result of the way this multiplication works, the matrix with a line of ones down what's called the 'leading diagonal' is the matrix equivalent of multiplying by one:

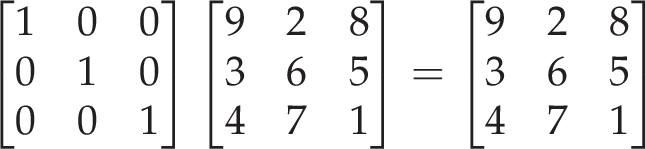
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 9 & 2 & 8 \\ 3 & 6 & 5 \\ 4 & 7 & 1 \end{bmatrix} = \begin{bmatrix} 9 & 2 & 8 \\ 3 & 6 & 5 \\ 4 & 7 & 1 \end{bmatrix}

Any matrix with this arrangement is called an identity matrix (represented often by the letter 'I'):

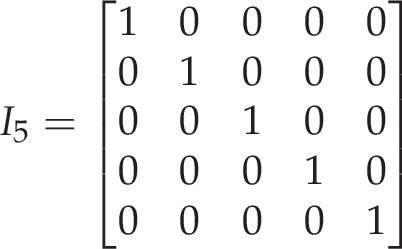
I_5=\begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}

Back to OpenGL

In OpenGL programming, matrices are used to express points in space, and also to transform these points. This is done through a 4x1 column matrix to express 3D points - the x, y, and z co-ordinates, and 'w', which is 1 if the matrix is a position, and 0 if its a direction:

\begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix}

Then, before points are 'used' (e.g. drawn), they are transformed by the currently active matrix, which is a 4x4 matrix. In older (now deprecated) OpenGL, the currently active matrix is set by a call to glMatrixMode, and is then usually initialised to the identity matrix via a call to glLoadIdentity. A fresh identity transformation matrix in OpenGL will look like the following:

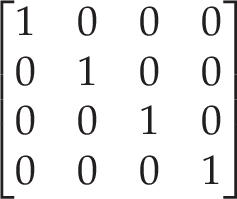
\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

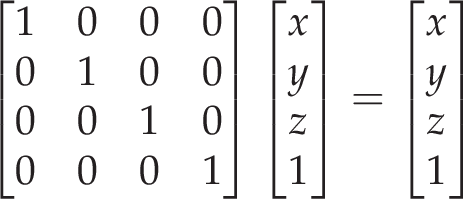
For this transformation to apply to a point, the point is simply pre-multiplied by the matrix. In this case, the transformation will have no impact on the point, which is great!

\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

Before we draw our point, however, we may well want to actually transform it in some way. In older versions of OpenGL, transformations were done through the now-deprecated glScale, glRotate, and glTranslate functions, and these functions changed the currently active matrix. So if we called glTranslate to move our point five units to the right, it'd result in the following multiplication to transform our point:

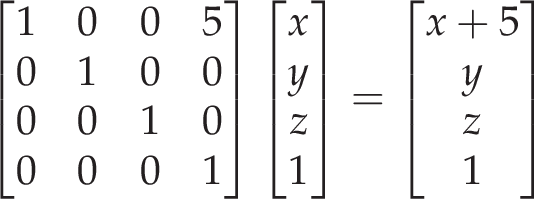
\begin{bmatrix} 1 & 0 & 0 & 5 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x+5 \\ y \\ z \\ 1 \end{bmatrix}

It works! What actually happened is that our currently active matrix was multiplied by the matrix representing a translation of five units in the 'x' direction, and then this transformed our point (which is what we saw above) to create the final point. If we call our point 'P' and our translation transformation 'T', then that means that $I_4 \times T \times P=P_1$ .

So, let's bring in another transformation, 'U', which scales our x-coordinate up by a factor of two. If we apply 'T', and then 'U', then our calculation for our final point becomes $I_4 \times T \times U \times P=P_1$ . Importantly, in that exact order; and remember, the order of multiplication with matrices does matter. We had our original fresh transformation matrix, multiplied this by 'T' with glTranslate, followed this with a multiplication by 'U' with glScale, and then the product of this with our point is the final point that is drawn.

You'd be forgiven if you thought that this meant that the translation occured, followed by the scale, but you'd be wrong. This becomes very clear if we bracket up all the multiplication we've done: $I_4 \times (T \times (U \times P)) = P_1$ , where in fact you can see that 'U' is applied first and then 'T', hence the seemingly backwards behaviour to what may have been intended by the order of function calls.

The composite transformation matrix , applies in the order .